Introduction
Some Initial Thoughts on Algorithmic Composition
Intuition
Repetition at a steady rate
Tempo-relative timing
Timed Counting
Counting through a List
Analysis of Some Patterns
That's Why They Call Them Digital Media
Linear change
Fading by means of interpolation
Randomness
Randomness and noise
Limiting the range of random choices
Moving range of random choices
A simple probabilistic decision
Probability distribution
Line-segment control function
Control function as a recognizable shape
Classic waveforms as control functions
Sine wave as control function
Pulse wave, a binary control function
Triangle wave as a control function
Discrete steps within a continuous function
First steps in modulating the modulator
Second steps in modulating the modulator
Modulating the modulators
Some Initial Thoughts on Visualizing Music
Thursday, September 24, 2009
Some Initial Thoughts on Visualizing Music
The variety of possible relationships between sound and image is a vast and intriguing subject. In terms of visualizing music, it can include music notation, spectrographic displays, paintings inspired by music, son et lumière, software that algorithmically generates animation based on sound, music videos, Schenkerian analyses, and so on. In terms of "sonifying" images there is music based on paintings, film music, music generated by drawing on film soundtrack, and a wide range of applications of sound used to display numerical data.
Traditional Western music notation attempts to visualize music by means of a symbolic language. Fluent readers of music notation can use it to recreate -- mentally and/or on an instrument -- the music described by that notation. However, such notation does not really try to give a visual analog of the music. Music notation systems are usually intended to a) give a performer a symbolic representation of some aspects of the music's structure and b) give an instructional tablature of how to produce the desired music on an instrument. The distinction between a and b is perhaps best illustrated by music for lute and guitar, which can be written as notes in standard notation or as fingerings in tablature. Notes are better for revealing the musical structure; fingerings are better for revealing the actions required to produce the sound on the instrument. To a greater or lesser degree, each of those two methods of notation serves both functions of description and instruction. But notation is in some ways incomplete and imprecise, and relies on a good deal of unstated cultural knowledge possessed by the reader -- particularly in its treatment of subtleties of timbre, dynamics, rubato, ornamental inflections, etc. Western notation is relatively precise in describing the pitch and rhythm of note events, but is less precise in visualizing the other parameters of musical structure or sonic content.
Digital audio workstation software provides a static amplitude-over-time graph of the sound wave itself. If one zooms in to look closely at a few milliseconds of the sound, one might be able to tell from the waveform whether the sound is periodic, approximately how rich in harmonics it is, or approximately how noisy it is, but since you're only viewing a tiny time segment of the sound, it's hard to know much of interest about its musical content. If one zooms out to look at several seconds of sound one can see its overall amplitude envelope and may thus be able to discern something about its loudness and rhythm, but details of its content are not apparent. It's an adequate visualization for recognizing significant events in the sound and for editing the sound accordingly, but is otherwise not very rich in information.
Likewise a spectrographic display, even an animated one that updates continually in real time, provides information about the frequency content, its harmonicity, inharmonicity, and noisiness, but still requires expert and painstaking analysis and interpretation to derive information about the musical structure.
The following discussion and example will focus on one particular type of visualization: using information derived from the sound or musical structure itself to generate an animation that displays and elucidates one or more aspects of the sonic/musical structure. In other words, visualization that is concerned not with creating an aesthetic object inspired by the music, but with displaying useful information for "understanding" or analyzing the sound.
To visualize music (as distinguished from visualizing sound), we need to focus on the musical attributes that are of particular interest for our purpose. The parameters most important for analyzing music can be many and varied, may be subject of disagreement, and may change as the music proceeds. There are the standard accepted fundamental musical parameters such as pitch, loudness, and duration, some more complex or derived parameters of musical sounds such as timbre, accent, and articulation, and more global attributes of a musical structure such as rhythmic patterns, tempo, event density, dissonance, spatial distribution, and so on. One way to think about music is as an evolving multidimensional entity, in which each dimension corresponds to a parameter or trait or attribute of interest.
How can you depict multi-dimensionality in a two-dimensional space? In addition to the obvious two dimensions, horizontal and vertical, we might consider the color, size, brightness, and shape of objects to be additional dimensions that can carry information. Three-dimensional graphics can give the impression of a third spatial dimension. The passage of time in the visualization generally will correspond to the musical time in a realtime depiction, but other relationships such as slowed-down time or frozen time might also be useful in some circumstances.
The designer/programmer of the visualization must decide what visual dimensions and characteristics most effectively convey musical attributes. For example, we say that pitches are "high" or "low", so we often find it best to depict pitch height in the vertical dimension. On the other hand, we know that in fact there's nothing inherently spatially higher or lower about one pitch relative to another. In some cases we might just as usefully map them to the horizontal dimension, as they appear on a piano keyboard, or to some other continuum. For some synesthetes with perfect pitch, pitch classes might correspond to particular hues. In a particular tuning system or scale system, pitches may be thought of as residing on a virtual grid. There might also be cases in which higher pitches might be deemed more intense or brighter, or lower pitches might be deemed darker or weightier. In short, mappings of sonic and musical attributes to visual dimensions and characteristics are quite subjective and case-dependent, even though many standard mappings exist.
In the program demonstrating counting through a list, one part of the program reads repeatedly through a list of sixteen MIDI pitch numbers. Another part of the program reads through a list of sixteen x,y locations for the display of a black dot. The mapping between the pitches and the dot locations is imprecise, but is still very suggestive of a correlation because the vertical height of the dot corresponds to the pitch height, so the dot seems to depict the pitch contour. The horizontal locations of the dot do not correspond to any specific parameter in the music, but they are chosen so as to suggest a generally circular pattern, thus enhancing the cyclic feeling of the pitch movement when the program counts repeatedly in a loop.
In the programs that demonstrate limiting and moving ranges of random values, pitch is again displayed in the vertical dimension as individual slider positions in a multislider object, and the image is scrolled continuously in the horizontal dimension to depict the passage of time and show the most recent several seconds' worth of note choices.
It's worth noting that in those examples the tempo and rhythm are constant, and are thus not of particular musical interest, so they are not displayed. The dynamics (the note velocities) are of some interest, but arguably of less interest than the pitches, so for the sake of simplicity there's no attempt to display that parameter either.
In the programs that show the first and second steps in modulating the modulator, the pitch of the sound changes in a continuous glissando instead of in discrete steps of the equal-tempered scale, so the pitch value is displayed in a scope~ object capable of displaying the (most recently played one second of the) pitch contour.
The program called "modulating the modulators" produces a sound in which a few different musical attributes are constantly and gradually changing. In that example it's pretty clear what's worth depicting in the sound, because we know what's being modified: the pitch, the volume and the panning (the left-right location). We know this because the computer itself is generating the sound, and we have access to the information that controls those particular parameters. These three parameters can be mapped to three dimensions or characteristics of an animated image.
Here is an example of one possible visualization of the pitch, volume, and panning of the sound generated in the "modulating the modulators" program. (The drawing objects are hidden in the program, but they're shown here in the graphic below.)
.jpg)
This program displays each musical note in terms of its most important attributes: its pitch contour, loudness, and panning. Pitch is shown in the vertical dimension, panning is shown in the horizontal dimension, and volume is shown in terms of the brightness of the note. Since the sound has only a single timbre, it seems reasonable to use a single color to draw the notes. These attributes change during the course of a single note, so the graphic display ends up being a line drawing that depicts the shape of those attributes during the note.
The fragment of the program shown in the picture above has three main focal points: the part that draws the image, the part that stores the image to be drawn, and the part that erases the previously drawn image at the start of each new note.
The drawing part consists of a metro object, a jit.matrix object named notes, and a jit.pwindow object. The dimensions of the jit.pwindow are 128x128 pixels, the same as the dimensions of the jit.matrix. The time interval of the metro is defined such that it will cause the contents of the jit.matrix to be drawn in the jit.pwindow 30 times per second, which is sufficiently often to give a sense of continuity to the animation. The metro gets turned on and off automatically at the same time as the audio is turned on and off, so it's always drawing whenever the sound is playing.
The jit.matrix object is being filled by a jit.poke~ object that refers to the same space in memory. The arguments of jit.poke~ indicate the name of the jit.matrix into which to poke signal values, the number of dimensions of the matrix that we want to access, and the plane number we want to access. (Plane 2 is the green color plane in a 4-plane char ARGB matrix; we're only using the color green.) The purpose of jit.poke~ is to use MSP signals to specify the values and locations to be drawn into the specified plane of the specified matrix. The inlets are, in order from left to right, for the value that will be stored (the brightness of green), the cell location in dimension 0 (the horizontal cell location), and the cell location in dimension 1 (the vertical cell location). The inlets are fed by signals that control volume, panning, and pitch -- the three musical attributes we want to depict. So volume is mapped to brightness, panning is mapped to horizontal location, and pitch is mapped to vertical location. The 128 vertical pixels are mapped to the 0-127 range of MIDI. The signal is first passed through a !-~ 127 object to create an inverse mapping of pitch to pixel number. That's because MIDI pitch values go up from 0 to 127 but cell indices in the matrix go down from 0 to 127. The panning value, which is originally expressed in the range 0 to 1 gets passed through a *~ 127 object to expand it to the horizontal range of the matrix, a range which was chosen for no other reason than to make it the same size as the vertical range. The volume value is originally in the range from 0 to -30 dB, so before it gets to jit.poke~ it gets multiplied by 0.03 to reduce its range to 0 to -0.9, and then has 1.0 added to it to yield brightness values that vary from 1.0 down to 0.1. The result of all of this is that the brightness value that corresponds to volume gets placed into plane 2 of every cell of the matrix that corresponds to a pitch and panning combination that occurs during a given note.
What I'm calling a "note" in this context is each time an amplitude envelope window is generated by the triangle function that modulates the amplitude of the signal coming directly out of the tri~ object in the synthesis patch. Those amplitude envelopes are controlled by the phasor~ that reads through just the first half of the triangle wave function stored in the buffer~. In the drawing portion of the patch you can see the use of the delta~ object to monitor the change in the signal coming from the phasor~. Since the phasor~ generates an upward ramp that goes cyclically from 0 to (almost) 1 and then leaps back to 0, there is a very specific moment, which occurs only at the beginning of each cycle, when the change in the phasor~, instead of being a slight increase, is suddenly a decrease (on the sample when it leaps back to 0). So you can use the <~ 0. object to detect when the change occurs, namely at the instant when delta~ outputs a negative sample value. At that moment the <~ 0. object will output a 1 (the only time the test succeeds), and the edge~ object will report that it occurred. That report is used to trigger a clear message to jit.matrix, causing it to set all its values to 0, effectively erasing the previous note from the matrix.
So in this example, the drawing rate or "refresh" rate of the visual display is 30 times per second, and the content of the display matrix is erased (reset to all 0) once per note. The passage of time is not displayed as a dimension in its own right, but rather by the constant updating of the display. The display changes according to the changing shape of the line being drawn as determined by the change in pitch and panning in the course of each note. This is a non-traditional way to display information about the musical structure, but it directly addresses the three main musical features of this particular sound.
Traditional Western music notation attempts to visualize music by means of a symbolic language. Fluent readers of music notation can use it to recreate -- mentally and/or on an instrument -- the music described by that notation. However, such notation does not really try to give a visual analog of the music. Music notation systems are usually intended to a) give a performer a symbolic representation of some aspects of the music's structure and b) give an instructional tablature of how to produce the desired music on an instrument. The distinction between a and b is perhaps best illustrated by music for lute and guitar, which can be written as notes in standard notation or as fingerings in tablature. Notes are better for revealing the musical structure; fingerings are better for revealing the actions required to produce the sound on the instrument. To a greater or lesser degree, each of those two methods of notation serves both functions of description and instruction. But notation is in some ways incomplete and imprecise, and relies on a good deal of unstated cultural knowledge possessed by the reader -- particularly in its treatment of subtleties of timbre, dynamics, rubato, ornamental inflections, etc. Western notation is relatively precise in describing the pitch and rhythm of note events, but is less precise in visualizing the other parameters of musical structure or sonic content.
Digital audio workstation software provides a static amplitude-over-time graph of the sound wave itself. If one zooms in to look closely at a few milliseconds of the sound, one might be able to tell from the waveform whether the sound is periodic, approximately how rich in harmonics it is, or approximately how noisy it is, but since you're only viewing a tiny time segment of the sound, it's hard to know much of interest about its musical content. If one zooms out to look at several seconds of sound one can see its overall amplitude envelope and may thus be able to discern something about its loudness and rhythm, but details of its content are not apparent. It's an adequate visualization for recognizing significant events in the sound and for editing the sound accordingly, but is otherwise not very rich in information.
Likewise a spectrographic display, even an animated one that updates continually in real time, provides information about the frequency content, its harmonicity, inharmonicity, and noisiness, but still requires expert and painstaking analysis and interpretation to derive information about the musical structure.
The following discussion and example will focus on one particular type of visualization: using information derived from the sound or musical structure itself to generate an animation that displays and elucidates one or more aspects of the sonic/musical structure. In other words, visualization that is concerned not with creating an aesthetic object inspired by the music, but with displaying useful information for "understanding" or analyzing the sound.
To visualize music (as distinguished from visualizing sound), we need to focus on the musical attributes that are of particular interest for our purpose. The parameters most important for analyzing music can be many and varied, may be subject of disagreement, and may change as the music proceeds. There are the standard accepted fundamental musical parameters such as pitch, loudness, and duration, some more complex or derived parameters of musical sounds such as timbre, accent, and articulation, and more global attributes of a musical structure such as rhythmic patterns, tempo, event density, dissonance, spatial distribution, and so on. One way to think about music is as an evolving multidimensional entity, in which each dimension corresponds to a parameter or trait or attribute of interest.
How can you depict multi-dimensionality in a two-dimensional space? In addition to the obvious two dimensions, horizontal and vertical, we might consider the color, size, brightness, and shape of objects to be additional dimensions that can carry information. Three-dimensional graphics can give the impression of a third spatial dimension. The passage of time in the visualization generally will correspond to the musical time in a realtime depiction, but other relationships such as slowed-down time or frozen time might also be useful in some circumstances.
The designer/programmer of the visualization must decide what visual dimensions and characteristics most effectively convey musical attributes. For example, we say that pitches are "high" or "low", so we often find it best to depict pitch height in the vertical dimension. On the other hand, we know that in fact there's nothing inherently spatially higher or lower about one pitch relative to another. In some cases we might just as usefully map them to the horizontal dimension, as they appear on a piano keyboard, or to some other continuum. For some synesthetes with perfect pitch, pitch classes might correspond to particular hues. In a particular tuning system or scale system, pitches may be thought of as residing on a virtual grid. There might also be cases in which higher pitches might be deemed more intense or brighter, or lower pitches might be deemed darker or weightier. In short, mappings of sonic and musical attributes to visual dimensions and characteristics are quite subjective and case-dependent, even though many standard mappings exist.
In the program demonstrating counting through a list, one part of the program reads repeatedly through a list of sixteen MIDI pitch numbers. Another part of the program reads through a list of sixteen x,y locations for the display of a black dot. The mapping between the pitches and the dot locations is imprecise, but is still very suggestive of a correlation because the vertical height of the dot corresponds to the pitch height, so the dot seems to depict the pitch contour. The horizontal locations of the dot do not correspond to any specific parameter in the music, but they are chosen so as to suggest a generally circular pattern, thus enhancing the cyclic feeling of the pitch movement when the program counts repeatedly in a loop.
In the programs that demonstrate limiting and moving ranges of random values, pitch is again displayed in the vertical dimension as individual slider positions in a multislider object, and the image is scrolled continuously in the horizontal dimension to depict the passage of time and show the most recent several seconds' worth of note choices.
It's worth noting that in those examples the tempo and rhythm are constant, and are thus not of particular musical interest, so they are not displayed. The dynamics (the note velocities) are of some interest, but arguably of less interest than the pitches, so for the sake of simplicity there's no attempt to display that parameter either.
In the programs that show the first and second steps in modulating the modulator, the pitch of the sound changes in a continuous glissando instead of in discrete steps of the equal-tempered scale, so the pitch value is displayed in a scope~ object capable of displaying the (most recently played one second of the) pitch contour.
The program called "modulating the modulators" produces a sound in which a few different musical attributes are constantly and gradually changing. In that example it's pretty clear what's worth depicting in the sound, because we know what's being modified: the pitch, the volume and the panning (the left-right location). We know this because the computer itself is generating the sound, and we have access to the information that controls those particular parameters. These three parameters can be mapped to three dimensions or characteristics of an animated image.
Here is an example of one possible visualization of the pitch, volume, and panning of the sound generated in the "modulating the modulators" program. (The drawing objects are hidden in the program, but they're shown here in the graphic below.)
.jpg)
This program displays each musical note in terms of its most important attributes: its pitch contour, loudness, and panning. Pitch is shown in the vertical dimension, panning is shown in the horizontal dimension, and volume is shown in terms of the brightness of the note. Since the sound has only a single timbre, it seems reasonable to use a single color to draw the notes. These attributes change during the course of a single note, so the graphic display ends up being a line drawing that depicts the shape of those attributes during the note.
The fragment of the program shown in the picture above has three main focal points: the part that draws the image, the part that stores the image to be drawn, and the part that erases the previously drawn image at the start of each new note.
The drawing part consists of a metro object, a jit.matrix object named notes, and a jit.pwindow object. The dimensions of the jit.pwindow are 128x128 pixels, the same as the dimensions of the jit.matrix. The time interval of the metro is defined such that it will cause the contents of the jit.matrix to be drawn in the jit.pwindow 30 times per second, which is sufficiently often to give a sense of continuity to the animation. The metro gets turned on and off automatically at the same time as the audio is turned on and off, so it's always drawing whenever the sound is playing.
The jit.matrix object is being filled by a jit.poke~ object that refers to the same space in memory. The arguments of jit.poke~ indicate the name of the jit.matrix into which to poke signal values, the number of dimensions of the matrix that we want to access, and the plane number we want to access. (Plane 2 is the green color plane in a 4-plane char ARGB matrix; we're only using the color green.) The purpose of jit.poke~ is to use MSP signals to specify the values and locations to be drawn into the specified plane of the specified matrix. The inlets are, in order from left to right, for the value that will be stored (the brightness of green), the cell location in dimension 0 (the horizontal cell location), and the cell location in dimension 1 (the vertical cell location). The inlets are fed by signals that control volume, panning, and pitch -- the three musical attributes we want to depict. So volume is mapped to brightness, panning is mapped to horizontal location, and pitch is mapped to vertical location. The 128 vertical pixels are mapped to the 0-127 range of MIDI. The signal is first passed through a !-~ 127 object to create an inverse mapping of pitch to pixel number. That's because MIDI pitch values go up from 0 to 127 but cell indices in the matrix go down from 0 to 127. The panning value, which is originally expressed in the range 0 to 1 gets passed through a *~ 127 object to expand it to the horizontal range of the matrix, a range which was chosen for no other reason than to make it the same size as the vertical range. The volume value is originally in the range from 0 to -30 dB, so before it gets to jit.poke~ it gets multiplied by 0.03 to reduce its range to 0 to -0.9, and then has 1.0 added to it to yield brightness values that vary from 1.0 down to 0.1. The result of all of this is that the brightness value that corresponds to volume gets placed into plane 2 of every cell of the matrix that corresponds to a pitch and panning combination that occurs during a given note.
What I'm calling a "note" in this context is each time an amplitude envelope window is generated by the triangle function that modulates the amplitude of the signal coming directly out of the tri~ object in the synthesis patch. Those amplitude envelopes are controlled by the phasor~ that reads through just the first half of the triangle wave function stored in the buffer~. In the drawing portion of the patch you can see the use of the delta~ object to monitor the change in the signal coming from the phasor~. Since the phasor~ generates an upward ramp that goes cyclically from 0 to (almost) 1 and then leaps back to 0, there is a very specific moment, which occurs only at the beginning of each cycle, when the change in the phasor~, instead of being a slight increase, is suddenly a decrease (on the sample when it leaps back to 0). So you can use the <~ 0. object to detect when the change occurs, namely at the instant when delta~ outputs a negative sample value. At that moment the <~ 0. object will output a 1 (the only time the test succeeds), and the edge~ object will report that it occurred. That report is used to trigger a clear message to jit.matrix, causing it to set all its values to 0, effectively erasing the previous note from the matrix.
So in this example, the drawing rate or "refresh" rate of the visual display is 30 times per second, and the content of the display matrix is erased (reset to all 0) once per note. The passage of time is not displayed as a dimension in its own right, but rather by the constant updating of the display. The display changes according to the changing shape of the line being drawn as determined by the change in pitch and panning in the course of each note. This is a non-traditional way to display information about the musical structure, but it directly addresses the three main musical features of this particular sound.
Labels:
attribute,
data,
display,
parameter,
sonification,
visualization
Friday, September 18, 2009
Modulating the modulators
A control function with a particular shape can serve a role similar to a traditional musical motive. Even when it is modified in duration, rhythm, or shape, its relation to the original remains evident and it serves to unify a larger composition. A motive or shape might be recognizable at different structural/temporal levels, in which case the form may take on a "fractal" or "self-similar" character.
In other chapters we've taken some first and intermediate steps to progressively increase the complexity of examples in which a control function modulates another modulator of the same shape, such that a single shaped is used at different formal levels in a somewhat self-similar manner.
Here's a more full blown example of a single control function used to modulate a sound at many formal levels, with modulators modulating other modulators, in this case including the parameters of pitch, note rate, volume, and panning (location).

The carrier sound is a triangle wave oscillator, in the tri~ object. The volume of that oscillator is continually modulated in a way that actually separates it into individual notes; it is windowed by a repeating triangular shape going from 0 to 1 and back to 0--the first half of the triangle function stored in the wavetable in the buffer~. The rate of those notes is itself modulated by a triangle function, varying from 1 to 15 notes per second every 25 seconds (the rate is varied up and down + and - 7 from a central rate of 8 Hz, by a triangle oscillator with a rate of 0.04 Hz).
The volume of the sound is further modulated by another triangular LFO that creates a swell and dip of + and - 15 dB in the overall volume every ten seconds, to give a periodic crescendo and diminuendo spanning 30 decibels, which is about as much as most instrumentalists do in practice, even though their instruments are often technically capable of a wider range of intensities.
The pitch of the sound is modulated in almost exactly the same way as was demonstrated in another article. The pitch glides in a triangular shape around a central pitch that is itself slowly changing in a triangular shape over a span of every 50 seconds. The rate of the glissandi varies from 1 to 15 Hz, varying triangularly in a 20-second cycle. The depth of the glissandi varies from + and - 0 to 12 semitones, controlled by a 15-second cycle (perceptually a 7.5-second cycle).
The perceived location of the sound pans back and forth between left and right controlled by a triangular function at a rate that varies from 1/16 Hz to 16 Hz -- quite gradually to quite quickly -- with the rate itself determined by a triangular cycle that repeats every 30 seconds, using the most common panning technique, known as "intensity panning". This takes advantage of the fact that one of the main indicators of the location of a sound's source is inter-aural intensity difference (IID), the balance of the sound's intensity in our two ears. The more the intensity of sound in one ear exceeds the intensity in the other ear, the more we are inclined to think the sound comes from that direction. Thus, varying the sound's intensity from 0 to 1 for one ear (or one speaker) as we vary the intensity from 1 to 0 in the other ear (or the other speaker) gives the impression of the sound being at different locations between the two ears (speakers). So a triangle wave with an amplitude of + and - 0.5, centered around 0.5 is used to vary the gain of the right audio channel, and 1 minus that value is used to determine the gan of the left audio channel. As one channel fades from 0 to 1, the other channel fades from 1 to 0, and vice versa.
Our sense of the distance of sound sources is complicated, but in general it's roughly proportional to the amplitude of the sound. So the same sound at half the amplitude would -- all other things being the same -- tend to sound half as close to us (that is, twice as distant). The perceived overall intensity of the sound will depend on the sum of the two audio channels. Perceived intensity is proportional to the square of the amplitude, and the perceived overall intensity is thus proportional to the sum of the squares of the amplitudes of the two channels. So if we want to keep the sound seeming to be the same distance from the listener as we pan from left to right, we need to keep the sum of the squares of their amplitudes the same. So, as a final step before output, we take the square root of the desired intensity for each channel, and use that as the gain control value for the channel. The picture below shows the gain values for the two channels as they are initially calculated by the triangle function (on the left) and then shows the actual gain values that will be used -- the square roots (on the right). The first is the desired intensity of the two channels, and the second is the actual amplitude for the two channels that's required to deliver that intensity as the virtual sound location moves between left and right.

In order to make the rate of panning span the desired range from 1/16 Hz to 16 Hz, we used the triangle function as the exponent of the base 2, using the pow~ object. As the triangle function (the exponent) varies from 0 to 4 to -4 to 0, the result will vary from 1 to 16 to 1/16 to 1. When the rate is less than about 1 Hz, the duration of each panning cycle is greater than 1 second, and we can follow the panning as simulated movement; when the rate is greater than 1 Hz, the complete left-right cycle of panning takes places in less than a second, up to as little as 1/16 of a second (62.5 ms), so we perceive it more as a sort of "location tremolo" sound effect.
So in this example program the triangle wave function was used in nine different ways:
1) as the carrier waveform
2) as a window (amplitude envelope) to make individual "note" events
3) to modulate the rate and duration of the notes
4) to create 10-second volume swells
5) to vary the central pitch of the oscillator
6) to make pitch glissandi around that central pitch
7) to vary the depth of those glissandi
8) to vary the rate of those glissandi
9) to vary the panning of the sound
In other chapters we've taken some first and intermediate steps to progressively increase the complexity of examples in which a control function modulates another modulator of the same shape, such that a single shaped is used at different formal levels in a somewhat self-similar manner.
Here's a more full blown example of a single control function used to modulate a sound at many formal levels, with modulators modulating other modulators, in this case including the parameters of pitch, note rate, volume, and panning (location).

The carrier sound is a triangle wave oscillator, in the tri~ object. The volume of that oscillator is continually modulated in a way that actually separates it into individual notes; it is windowed by a repeating triangular shape going from 0 to 1 and back to 0--the first half of the triangle function stored in the wavetable in the buffer~. The rate of those notes is itself modulated by a triangle function, varying from 1 to 15 notes per second every 25 seconds (the rate is varied up and down + and - 7 from a central rate of 8 Hz, by a triangle oscillator with a rate of 0.04 Hz).
The volume of the sound is further modulated by another triangular LFO that creates a swell and dip of + and - 15 dB in the overall volume every ten seconds, to give a periodic crescendo and diminuendo spanning 30 decibels, which is about as much as most instrumentalists do in practice, even though their instruments are often technically capable of a wider range of intensities.
The pitch of the sound is modulated in almost exactly the same way as was demonstrated in another article. The pitch glides in a triangular shape around a central pitch that is itself slowly changing in a triangular shape over a span of every 50 seconds. The rate of the glissandi varies from 1 to 15 Hz, varying triangularly in a 20-second cycle. The depth of the glissandi varies from + and - 0 to 12 semitones, controlled by a 15-second cycle (perceptually a 7.5-second cycle).
The perceived location of the sound pans back and forth between left and right controlled by a triangular function at a rate that varies from 1/16 Hz to 16 Hz -- quite gradually to quite quickly -- with the rate itself determined by a triangular cycle that repeats every 30 seconds, using the most common panning technique, known as "intensity panning". This takes advantage of the fact that one of the main indicators of the location of a sound's source is inter-aural intensity difference (IID), the balance of the sound's intensity in our two ears. The more the intensity of sound in one ear exceeds the intensity in the other ear, the more we are inclined to think the sound comes from that direction. Thus, varying the sound's intensity from 0 to 1 for one ear (or one speaker) as we vary the intensity from 1 to 0 in the other ear (or the other speaker) gives the impression of the sound being at different locations between the two ears (speakers). So a triangle wave with an amplitude of + and - 0.5, centered around 0.5 is used to vary the gain of the right audio channel, and 1 minus that value is used to determine the gan of the left audio channel. As one channel fades from 0 to 1, the other channel fades from 1 to 0, and vice versa.
Our sense of the distance of sound sources is complicated, but in general it's roughly proportional to the amplitude of the sound. So the same sound at half the amplitude would -- all other things being the same -- tend to sound half as close to us (that is, twice as distant). The perceived overall intensity of the sound will depend on the sum of the two audio channels. Perceived intensity is proportional to the square of the amplitude, and the perceived overall intensity is thus proportional to the sum of the squares of the amplitudes of the two channels. So if we want to keep the sound seeming to be the same distance from the listener as we pan from left to right, we need to keep the sum of the squares of their amplitudes the same. So, as a final step before output, we take the square root of the desired intensity for each channel, and use that as the gain control value for the channel. The picture below shows the gain values for the two channels as they are initially calculated by the triangle function (on the left) and then shows the actual gain values that will be used -- the square roots (on the right). The first is the desired intensity of the two channels, and the second is the actual amplitude for the two channels that's required to deliver that intensity as the virtual sound location moves between left and right.

In order to make the rate of panning span the desired range from 1/16 Hz to 16 Hz, we used the triangle function as the exponent of the base 2, using the pow~ object. As the triangle function (the exponent) varies from 0 to 4 to -4 to 0, the result will vary from 1 to 16 to 1/16 to 1. When the rate is less than about 1 Hz, the duration of each panning cycle is greater than 1 second, and we can follow the panning as simulated movement; when the rate is greater than 1 Hz, the complete left-right cycle of panning takes places in less than a second, up to as little as 1/16 of a second (62.5 ms), so we perceive it more as a sort of "location tremolo" sound effect.
So in this example program the triangle wave function was used in nine different ways:
1) as the carrier waveform
2) as a window (amplitude envelope) to make individual "note" events
3) to modulate the rate and duration of the notes
4) to create 10-second volume swells
5) to vary the central pitch of the oscillator
6) to make pitch glissandi around that central pitch
7) to vary the depth of those glissandi
8) to vary the rate of those glissandi
9) to vary the panning of the sound
Labels:
control,
function,
intensity,
modulation,
motive,
panning,
self-similarity,
triangle
Thursday, September 17, 2009
Second steps in modulating the modulator
Here are two programs that show further development of the programs described in first steps in modulating the modulators. There we saw how to use an LFO to modulate the pitch of a carrier, and how to use another LFO at an even slower rate to modulate the amplitude of the modulator.
In this first example we modulate both the rate and the depth (the frequency and the amplitude) of the LFO that is modulating the pitch of the carrier oscillator.
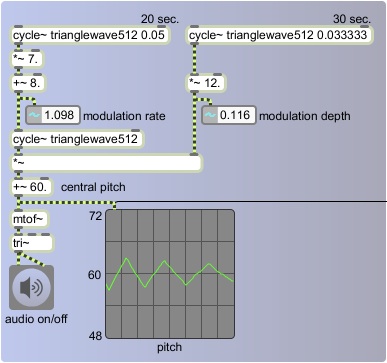
Once again we use all triangle functions, and we use a central pitch of 60 (middle C). The depth of pitch modulation -- plus or minus a certain number of semitones -- changes continuously, determined by the instantaneous value of a very-low-frequency oscillator with a peak amplitude of 12. Therefore, the depth will be as great as + or - 12 semitones, or as little as 0. The rate of the modulation varies from 1 Hz to 15 Hz, controlled by very-low-frequency oscillator that has a peak amplitude of 7 and an offset of 8 (so it varies up to + or - 7 Hz around its central rate of 8 Hz). Because these two control functions have different periodicities, the effect is continually changing, repeating exactly every 60 seconds.
In the next example we add one more modulator to continually change the central pitch, varying it up to + and - 30 semitones around a center of 66.
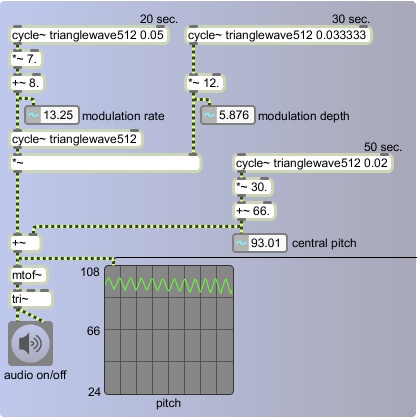
The central pitch will slowly, over the course of 50 seconds, rise from 66 to 96, fall to 36, then rise again to 66. The actual moment-to-moment pitch will oscillate up to 12 semitones around that, so the true pitch at any given instant could be as low as 24 or as high as 108, roughly the range of a piano. Since all three of these control functions have different periodicities -- 20, 30, and 50 seconds -- the entire cycle only repeats exactly every 5 minutes.
It's worth noting that as we combine different long cyclic phenomena with different periodicities -- in this case 20, 30, and 50 seconds -- the result of their combination varies continuously over a longer period that's equal to the product of the prime factors of the periods -- in this case 2 times 2 times 3 times 5 times 5 = 300 seconds. The effect is one of something that remains the same -- after all, it's the same three cycles repeating precisely over and over -- yet always seems slightly different because the juxtaposition and relationship of the cycles is always changing. This phenomenon is an essential component of much "minimal" or "phase" music.
In this first example we modulate both the rate and the depth (the frequency and the amplitude) of the LFO that is modulating the pitch of the carrier oscillator.

Once again we use all triangle functions, and we use a central pitch of 60 (middle C). The depth of pitch modulation -- plus or minus a certain number of semitones -- changes continuously, determined by the instantaneous value of a very-low-frequency oscillator with a peak amplitude of 12. Therefore, the depth will be as great as + or - 12 semitones, or as little as 0. The rate of the modulation varies from 1 Hz to 15 Hz, controlled by very-low-frequency oscillator that has a peak amplitude of 7 and an offset of 8 (so it varies up to + or - 7 Hz around its central rate of 8 Hz). Because these two control functions have different periodicities, the effect is continually changing, repeating exactly every 60 seconds.
In the next example we add one more modulator to continually change the central pitch, varying it up to + and - 30 semitones around a center of 66.

The central pitch will slowly, over the course of 50 seconds, rise from 66 to 96, fall to 36, then rise again to 66. The actual moment-to-moment pitch will oscillate up to 12 semitones around that, so the true pitch at any given instant could be as low as 24 or as high as 108, roughly the range of a piano. Since all three of these control functions have different periodicities -- 20, 30, and 50 seconds -- the entire cycle only repeats exactly every 5 minutes.
It's worth noting that as we combine different long cyclic phenomena with different periodicities -- in this case 20, 30, and 50 seconds -- the result of their combination varies continuously over a longer period that's equal to the product of the prime factors of the periods -- in this case 2 times 2 times 3 times 5 times 5 = 300 seconds. The effect is one of something that remains the same -- after all, it's the same three cycles repeating precisely over and over -- yet always seems slightly different because the juxtaposition and relationship of the cycles is always changing. This phenomenon is an essential component of much "minimal" or "phase" music.
Subscribe to:
Posts (Atom)
