Moving range of random choices

The previous example used a very slow metronome to cause a change in the music every five seconds -- specifically to choose a new range of random pitch numbers for the note-playing algorithm. Because the change happens suddenly at a specific moment in time, the change in the musical texture is abrupt, creating a distinct new block of notes every five seconds.

Just as we used linear interpolation in earlier chapters to play a scale from one pitch to another or to create a fade-in of loudness or brightness, we could also use linear interpolation to cause more gradual change in the range of random numbers being used in a decision making process. Instead of changing the range and offset of the random numbers abruptly, we could just as well interpolate from the current range settings to the new range settings over a period of time.

This patch is in some ways very similar to the previous one, but the big difference here is the introduction of the line object to make a gradual transition to a new range of random numbers over time.

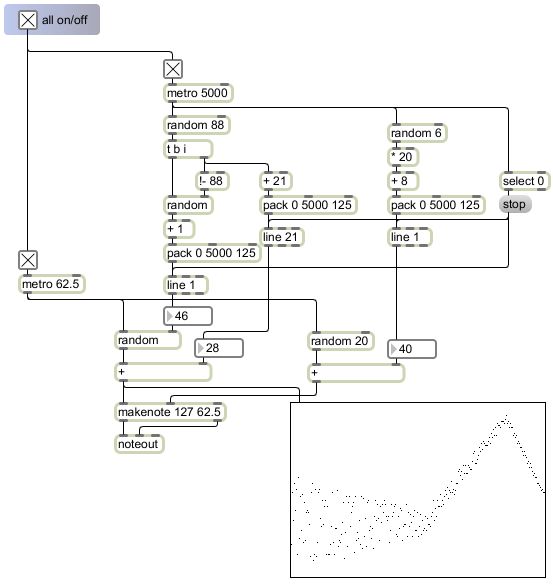Instead of the new ranges going directly to the right inlet of the + object and the random object, they go to line objects, which send out a changing series of numbers that move to the new value over the course of five seconds. The pack objects are there to make well-formed messages for the line objects, telling line what transition time to use (5000 ms) and how often to send out an intermediate number (every 125 ms).

As in the previous example, the random 88 object chooses the offset from the bottom of the piano keyboard, which will have 21 added to it and be used as the minimum value for the random range. That same number also is subtracted from 88 to set the maximum possible size of the randomly chosen pitch range, so as not to exceed the total range of the piano; the range size that actually gets chosen is thus some random number up to that maximum.

This patch also differs from the previous one in that it varies the MIDI velocities of the notes as well as the pitches, to create some dynamic variation of loudness. To do this, the program chooses one of only six possible ranges (with the random 6 object), which one might think of as being analogous to the musical dynamic markings pp, p, mp, mf, f, and ff. Those random numbers 0 to 5 are multiplied by 20 and added to 8, so that the possible offsets for the velocity range are 8, 28, 48, 68, 88, and 108. The size of the velocity range is always 20 (as determinied by the random 20 object) so there will always be the same range of variety in the velocities, but the range itself will almost always be moving continuously up or down because of the changing offset.

The transition time of 5000 ms for all of the line objects performing the gradual range changes was chosen to be the same as the interval of the metro object that is triggering the changes. However, the transition time could in fact be chosen to be quicker, all the way down to 0 ms for an immediate change. The interval of change choices by the metro and the transition time for the line objects have been set equal in this example so that the changes are constant and completely gradual, but in fact the two things could be treated as independent (that is, changes could be sometimes sudden and other times gradual).

There are still many more ways in which the musical form and texture could be varied in this sort of simple random decision making algorithm. For example, the rate of the note-playing metro could be varied continuously in a manner similar to the way pitch and velocity are being varied here, which would cause acceleration and deceleration of the note rate. It would also be possible to randomly change the time interval of the choice-making metro in order to to vary the frequency with which new choices are made. Also, currently all note durations are the same as the inter-onset interval between notes; one can thus say that the ratio of duration to IOI is 1. However, an algorithm could include random variation of that ratio describing note duration as a factor of the inter-onset interval, to create either staccato notes (silence between notes) if the factor is less than 1, or overlapping notes if the factor is greater than 1. We'll see use of this legato factor in a future example. There could also be a part of the algorithm for making random decisions about presses of the piano's sustain pedal (MIDI controller number 64). Obviously musical composition usually involves much more than just decisions about pitch and loudness.

This example and the previous one have shown how changes in the range of possibilities can create interesting variation even with simple random decisions, and that the changes can be either abrupt or gradual for different effects. These principles of controlling the size and offset of crucial ranges are useful even when dealing with non-random decision making.