Mathematically, randomness is characterized by a complete lack of discernible pattern, and equal probability of all possibilities. When we choose numbers at random at the audio sampling rate and listen to the resulting signal, it sounds to us like incomprehensible static: white noise. A spectral measurement of that sound would show essentially equal power at all frequencies. That is why it's called "white" noise; like white light, it contains all perceptible frequencies equally.
Cognitively, things that seem to us to have no pattern, organization, or reason for being as they are are often incomprehensible to us. When sound seems to us to have no pattern or organization--that is, when we find it incomprehensible--we might find it uninteresting or even irritating. Sound that is deemed irritating or unwanted by someone is often termed noise. However, it might be that there is in fact a pattern or organization, but it is simply too complicated for a particular listener to understand, and thus would be considered noise by that person.
When something strikes you as incomprehensible noise, consider the possibility that it may actually have a very interesting underlying organization, but that that organization is simply unknown to you or is too complex for you to understand given your current knowledge. That can be an encouraging thought, because it means that with the proper education you can understand it and perhaps then appreciate it better.
Composer and philosopher John Cage, in his discourse "The Future of Music: Credo" in Silence: Lectures and Writings, says "Wherever we are, what we hear is mostly noise. When we ignore it, it disturbs us. When we listen to it, we find it fascinating." In fact, a pretty good working definition of noise, from a philosophical and cognitive standpoint, might be "unwanted sound", or more generally, to take it beyond the realm of only sound, "unwanted stuff". This implies that if one can get rid of expectation or desire of what sounds we "want" or what sound "should" be, then unwanted sound, irritating and annoying sound, will cease to exist.
There is another sense in which the word noise can be related to digital arts. In theoretical discourse about communication and information, the word noise is used in the sense of "extraneous content" introduced during transmission of a message (and thus usually unwanted). The noise in this sense is clearly defined as the difference between the information at its source (whence it is transmitted) and the information at its destination (where it is received). In the case of sound, we can take this word "difference" by its mathematical meaning; we can literally determine the noise by subtracting the source sound from the destination sound. This fact is used for noise reduction in sound transmission, such as in the use of balanced lines for analog audio, or in the use of digitized (PCM) audio for recording and telecommunications. It can also be used to evaluate the imprecision of a quantization process. For example, the "quantization noise" introduced by digitizing sound is the difference between the analog sound at the input and its digitized representation used to produce the output. That noise is generally white noise, caused by random imprecision in the measurement and digitization of every single sound sample.
Sounds that lack pattern--either at the microscopic level of the sound wave itself or at the more macroscopic level of the organizations of different sounds--are characterized as noise. In that sense, all sounds can be situated on a continuum from totally simple (such as a sine tone) or predictable (a regularly repeating sound) to totally complex (to the point of incomprehensibility) and unpredictable (white noise, or random organizations of sounds). Sounds that are characterized as noisy in this way, such as drums and cymbals, which are situated on the noisy end of the continuum, are still musically useful and desirable, and sounds that are in the middle of the continuum, such as a breathy flute note which has both coherent sinusoidal components and random noise components due to air turbulence at the embouchure, can be very beautiful. So when used in this way, the characterization of a sound as "noise" is not a judgement of its desirability or lack thereof, but rather an evaluation of the amount of pattern and coherency it exhibits.
The pseudo-random numbers generated by a computer are actually derived by a systematic process. However, the process is so complicated and meaningless to us that we consider the results random. We can't follow the workings of the process in our heads, and even if we could, we probably wouldn't find that process and the patterns it generates to be meaningful or interesting. So it really is appropriate to think of a computer's pseudo-randomly generated numbers as random for our practical purposes.
In the previous examples, we used random decision making by the computer to choose from among a set of coherently related and moderately interesting possibilities: a set of twelve related musical chords, a set of six related images by the same painter, and a set of five sound files that all came from the same musical instrument. So the organization and aesthetic coherency that the composer/programmer put into the program is easily apparent when we run the program, but the ordering of the elements does not seem to have any sense of purpose or meaning because there genuinely is none; the ordering is random.
If the set of elements being chosen is stylistically neutral or unrelated, then we get an even less intentional effect because there is even less aesthetic control exerted by the programmer. Here is a program that shows some direct uses of random numbers to generate sound, music, and image, with almost no stylistic judgement or taste exerted by the programmer.
Of course, every decision, no matter how trivial or banal, is a judgement of some kind, and aimlessness or randomness or lack of personality could even be a desired trait in certain circumstances. In such cases, blatant exposition of randomness can be a useful means to that end. The point of these examples is to show randomness as a means of choosing a patternless series of values for sonic or visual characteristics that can only really be made meaningful by their organization. The result, as one might expect, is about as lacking in pattern as can be achieved from a steady stream of numbers.
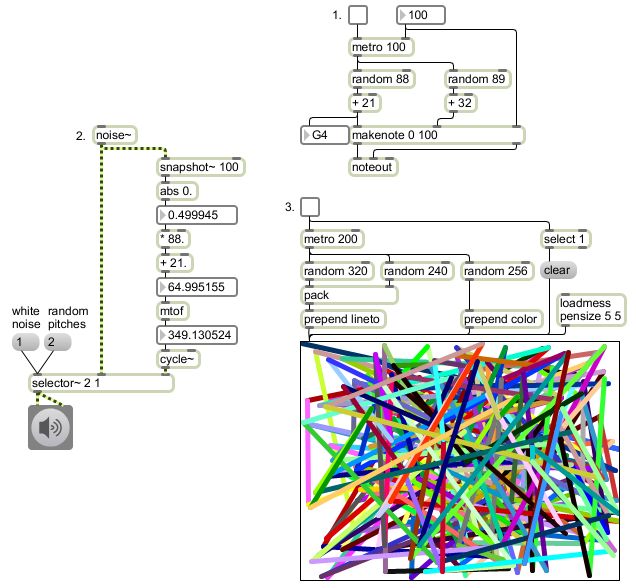
In program No. 1, the program regularly chooses at random from one of 88 MIDI pitch possibilities and 89 MIDI velocity (loudness) possibilities. To put the numbers coming from the random objects into a useful range, we add an offset to them. The notes are offset by 21 to put them in the range of a piano (21 to 108) and the velocities are offset by 32 to put them in a range compatible with most synthesizers that expresses soft to loud (32 to 120). There is no patten to the sequences of pitches and loudnesses, and no relationship between them. Cognitively, we might "stream" the events into different levels or categories (such as the very loud notes, or the very low notes, etc.), based on gestalt psychology principles of perception such as proximity and good continuation, but any perception of pattern that we may have is coincidental rather than intentional.
Program No. 2 uses the MSP noise~ object to produce a constant stream of random numbers between -1 and 1 at the audio sampling rate (most commonly 44,100 samples per second). If you listen to that directly, it sounds like static. If you click on the message box with the number 2, to open up the second signal inlet of the selector~, you will hear a simple sinusoidal tone, but with randomly chosen frequency changing every 1/10 second. The snapshot~ 100 object samples the random noise stream once every 100 milliseconds, the abs 0. object forces the numbers to be non-negative, and then those numbers between 0 and 1 are scaled by 88.0 and offset by 21.0 to make a pitch selection in MIDI-like terms, which then gets converted by the mtof object into a frequency value for the cycle~ object. All of those objects handle the numbers as floating-point values, so that the fractional part of the number is preserved. This means that the cycle~ object can really play any of about a billion possible frequencies within the range of the piano, rather than just the 88 notes of the equal-tempered scale as in the MIDI example. If you wanted to limit it to the 88 notes of the equal-tempered scale, you could simply remove the decimal point from the + 21. object, which would cause that object to throw away the fractional portion of its result.
Program No. 3 uses random choices of color from the object's standardized palette of 256 colors, and chooses a random point (x and y coordinates chosen at random) to which to draw a straight line using that color. Since all of the ranges needed for this procedure start at 0 (0-255 for color, and 0-319 and 0-240 for x and y), there's no need to add an offset. The integers chosen by the random objects are immediately applicable for use in messages to the lcd object.
Notice that in all three of these examples, the range of the random numbers has been limited to keep the numbers within a range of "reasonable" choices. For example, the musical notes are kept within the range of a piano; exceptionally low or high notes, or exceptionally loud or soft ones are not permitted. For that matter, in the example that employs MIDI, the pitches are also limited within the equal-tempered twelve-tone scale. The random values of the noise~ object are automatically kept within the range from -1 to 1 expected by the DAC, which also happens to be an easily scalable range. To use those values for choosing frequencies, the range is scaled and offset to be in the range of the piano (although not limited to equal temperament as in the MIDI example). In the visual example, position coordinates are limited to stay within the size of the drawing area; lines do not go toward any offscreen locations. The colors are chosen from among a set palette of 256 possibilities. So just by choosing the ranges of the random numbers, the programmer has exerted a little "artistic" discretion, by deciding what constitutes a "reasonable" value in each situation.
The timing of events in each example -- as in all the examples given so far -- is constant, giving a mechanistic feeling to the programs. There is no reason, however, that the timing intervals, too, couldn't be subjected to random choices of values, introducing unpredictability into the time dimension as well.
These examples can be thought of as showing randomness and random decision making in a raw and relatively unadulterated form. In many future examples we'll continue to use randomness and noise to show how random numbers can be limited, controlled, weighted, and filtered to get more meaningful--yet still not fully predictable--results.

No comments:
Post a Comment