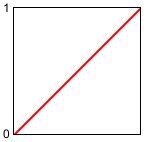
As shown in other chapters, a straight line function has many uses. When normalized as a ramp from 0 to 1, it's easy to enlarge it or contract it (with multiplication) and move it to a desired range (with addition) and even change its direction (by multiplying it by -1 or subtracting it from 1). The phasor~ object in Max provides a signal that ramps repeatedly from 0 to 1 at whatever frequency you specify.
This repeating ramp effectively creates a "sawtooth" function. By scaling it and offsetting it -- for example, by multiplying it by 220 and adding 220 to it -- we get a repeating ramp from 220 to 440 that can act as a control function for the frequency input of a carrier oscillator.
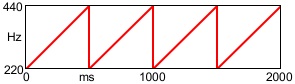 This example program uses a sawtooth function to make repeating frequency glissandi from 220 Hz to 440 Hz 2 times per second, using a phasor~.
This example program uses a sawtooth function to make repeating frequency glissandi from 220 Hz to 440 Hz 2 times per second, using a phasor~.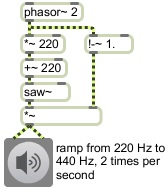 It uses the same phasor~ object to generate a simple amplitude envelope that goes immediately to 1 and ramps down to 0 at the same time as each glissando occurs.
It uses the same phasor~ object to generate a simple amplitude envelope that goes immediately to 1 and ramps down to 0 at the same time as each glissando occurs.The carrier oscillator (the oscillator that generates the signal that we actually listen to) is also a sawtooth waveform. A sawtooth waveform produces a harmonic spectrum, with the amplitude of each harmonic inversely proportional to the harmonic number. Thus, if the waveform has amplitude A, the fundamental (first harmonic) has amplitude A, the second harmonic has amplitude A/ 2, the third harmonic has amplitude A/3, etc. This means that when the fundamental frequency is 440 Hz -- and when the audio sampling rate is 44,100 Hz -- harmonics above the 50th will be above the Nyquist frequency, yet will have an amplitude that is, in many cases, still audible. (The 51st harmonic will have an amplitude about 34 dB less than the fundamental.) Those upper partials will cause aliasing, so when a sawtooth waveform is desired for a carrier oscillator, an ideal sawtooth wave such as that generated by phasor~ is not always the best choice. In Max, there is an object called saw~ that generates a wave with a spectrum very similar to a sawtooth, but that only produces audible harmonics up to the Nyquist frequency. So for the carrier oscillator we use the band-limited sawtooth sound of saw~ rather than the ideal sawtooth wave of phasor~.
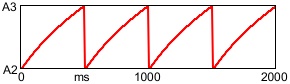
So in this simple example, we use a sawtooth waveform as the carrier signal, we modulate its frequency with a low-frequency sawtooth wave, and we use an inverted sawtooth wave at the same rate to generate amplitude envelopes that start loud and fade to 0. The result is repeating notes that glide up from 220 Hz to 440 Hz as the amplitude ramps from 1 to 0.
N.B. Because the glissandi are linear in frequency, they will actually be perceived as a logarithmic curve in terms of pitch.

No comments:
Post a Comment