First steps in modulating the modulator

Classic waveforms can be used to shape music synthesis, and that idea can be extended to shape musical composition with simple, recognizable, repeating shapes. Indeed, many figures that we think of as traditional pitch patterns in pre-electronic music have a direct correlation with those classic waveforms. The picture below exemplifies simple melodic patterns in traditional notation that could be achieved with discrete sampling of classic waveforms at low frequency, used to control the pitch of a carrier sound.


These melodic figures and their corresponding control functions can be described as:
1) trill, pulse wave
2) fingered tremolo, pulse wave with increased amplitude of modulation
3) glissando, linear ramp
4) scale, discrete sampling of a linear ramp
5) vibrato, triangle or sinusoid with low amplitude of modulation
6) up-down arpeggio, discrete sampling of a triangle function with high amplitude of modulation
7) melodic sequence, sawtooth (or any other shape) that is itself modulated by a ramp function
8) motivic melodic figure, discrete sampling of an arbitrary shape as it changes over time
9) up-down arpeggio (variation), discrete sampling of a sinusoidal function
You can probably imagine many other similar melodic shapes that are similarly simple yet effective.

These examples show clearly how a melody can be thought of as pitch modulation by a control function, and the shape can be simple, as in most of these examples, or more complex, as in example 8 above.

Sometimes more interesting effects can be achieved by using using these shapes operating at different formal levels at the same time, or with one shape modulating another as in example 7 above.

The triangle function, while decidedly not the most interesting shape imaginable, is particularly recognizable, and therefore is good for exemplifying these principles clearly. So we'll use it in a variety of examples for shaping sound synthesis and composition, focusing particularly on modulating one control function with a lower-frequency version of itself, which is to say, shaping the sound at a different formal levels, by means of self-similar use of a single shape.

The example below shows the most basic use of the triangle waveform as both a carrier oscillator and as a low-frequency control function for the pitch of that oscillator. The carrier oscillator generates a triangular waveform with the tri~ object which, instead of producing an ideal triangle function, protects against producing partials that will exceed the Nyquist frequency. The pitch of that oscillator is modulated by a low-frequency oscillator -- a cycle~ object reading from a wavetable that has been filled with one cycle of a triangle function. (When the patch is first opened, the small part of the program on the right fills the buffer~ with the values needed to make the stored triangle function. It also sets the scope~ to show one second of sound per display; the scope~ refreshes its display every 344 buffers of 128 samples.)


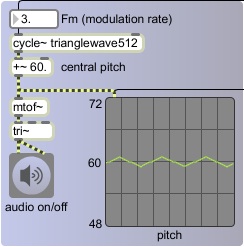
The modulating oscillator has a rate of 3 Hz, so the pitch of the carrier oscillator completes 3 cycles of the triangular shape per second. Since the amplitude of the cycle~ object is 1, the pitch fluctuates + and - 1 semitone around the central pitch of 60 (middle C). We'll call the rate of modulation Fm (pronounced "F sub m", meaning the frequency of the modulator), which is 3 Hz in this case, and we'll call the depth of modulation Am (pronounced "A sub m", meaning the amplitude of the modulator), which is constant at 1 in this case.

We can vary the pitch modulation over a longer period of time by modulating Fm and/or Am with an even slower oscillator. For example, in the program below we use one very-low-frequency oscillator to modulate the amplitude of a low-frequency oscillator that is modulating the pitch of the carrier oscillator.

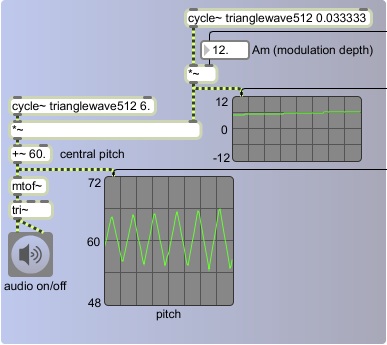We have set Fm to a constant of 6 Hz, but Am is modulated by another oscillator with a rate of 1/30 Hz and an amplitude of 12. So every 30 seconds the depth of the "vibrato" changes, according to the triangle wave function, from 0 semitones to 12, to 0 to -12 and back to 0. You probably won't recognize the difference between a vibrato depth of + and - 12 semitones and its inverse, + or - -12 semitones, so in effect the vibrato seems to complete a full cycle of expansion and contraction once every 15 seconds.

So the pitch modulation, with a rate of 6 Hz, is itself modulated in amplitude repeatedly every 15 seconds. This is a simple case of a a modulator modulating a modulator.