Second steps in modulating the modulator

Here are two programs that show further development of the programs described in first steps in modulating the modulators. There we saw how to use an LFO to modulate the pitch of a carrier, and how to use another LFO at an even slower rate to modulate the amplitude of the modulator.

In this first example we modulate both the rate and the depth (the frequency and the amplitude) of the LFO that is modulating the pitch of the carrier oscillator.


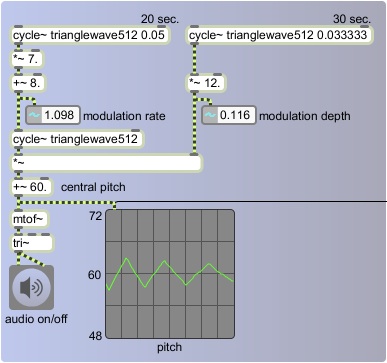
Once again we use all triangle functions, and we use a central pitch of 60 (middle C). The depth of pitch modulation -- plus or minus a certain number of semitones -- changes continuously, determined by the instantaneous value of a very-low-frequency oscillator with a peak amplitude of 12. Therefore, the depth will be as great as + or - 12 semitones, or as little as 0. The rate of the modulation varies from 1 Hz to 15 Hz, controlled by very-low-frequency oscillator that has a peak amplitude of 7 and an offset of 8 (so it varies up to + or - 7 Hz around its central rate of 8 Hz). Because these two control functions have different periodicities, the effect is continually changing, repeating exactly every 60 seconds.

In the next example we add one more modulator to continually change the central pitch, varying it up to + and - 30 semitones around a center of 66.


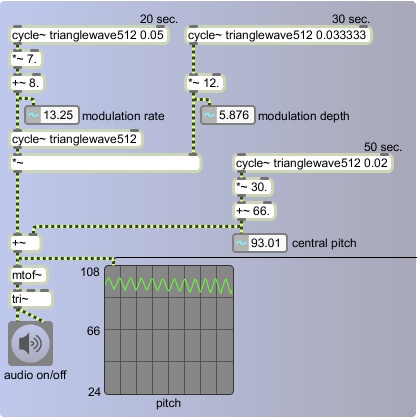
The central pitch will slowly, over the course of 50 seconds, rise from 66 to 96, fall to 36, then rise again to 66. The actual moment-to-moment pitch will oscillate up to 12 semitones around that, so the true pitch at any given instant could be as low as 24 or as high as 108, roughly the range of a piano. Since all three of these control functions have different periodicities -- 20, 30, and 50 seconds -- the entire cycle only repeats exactly every 5 minutes.

It's worth noting that as we combine different long cyclic phenomena with different periodicities -- in this case 20, 30, and 50 seconds -- the result of their combination varies continuously over a longer period that's equal to the product of the prime factors of the periods -- in this case 2 times 2 times 3 times 5 times 5 = 300 seconds. The effect is one of something that remains the same -- after all, it's the same three cycles repeating precisely over and over -- yet always seems slightly different because the juxtaposition and relationship of the cycles is always changing. This phenomenon is an essential component of much "minimal" or "phase" music.