Discrete steps within a continuous function

A series of discrete events can give the impression of a continuous progression. For example, the series of numbers 0, 2, 4, 6, 8, ... gives the impression of a straight linear progression, even though the series doesn't contain all the possible numbers along that line.

In fact, in digital media everything is a discrete step. Continuous phenomena are simulated by using a sufficiently high resolution of discrete steps. In digital video, for example, two-dimensional space is divided up into individual pixels, with each pixel having a color that is one of 16,777,216 discrete possibilities, time (the changing of the pixel values) is divided into 30 frames per second, and the audio stream is made up of 44,100 discrete amplitude values per second, with the instantaneous amplitude being one of 65,536 possible values.

A musical scale is another example of this. Like a ladder, a scale is a series of discrete steps in a linear progession. Even when the scale is not precisely linear, as in the case of a diatonic scale (steps 0, 2, 4, 5, 7, 9, 11, ... of the 12-tone chromatic scale), it still creates an impression of linear motion.

A smooth linear pitch glissando in computer music is achieved when the pitch value is changed continuously by a constant amount, usually as often as every single sample of the audio stream. If we employ the same control function but use it to change the frequency of the oscillator less frequently -- say, only a few times per second -- the pitch will stay steady for a longer time, and we'll perceive the discrete steps. Instead of changing the pitch 44,100 times per second, we could try using only 12 of those pitch values per second and holding the pitch steady in between.

This technique of transforming a high-resolution stream of numbers into a lower-resolution stream is known as "downsampling" -- reducing the rate or resolution of the discrete samples. In this case we want to reduce a stream of 44,100 samples per second to a series of only 12 samples per second. This process is achieved in audio with a technique called "sample and hold" -- in response to a triggering event, a single sample is held constant until the next trigger.

In Max, one way of doing this with an audio stream is with the sah~ object. A signal in the left inlet is sampled and held every time that the signal in the right inlet surpasses a particular threshold value.

This program uses sample and hold to turn a continuous pitch glissando function into a series of discrete scale steps.

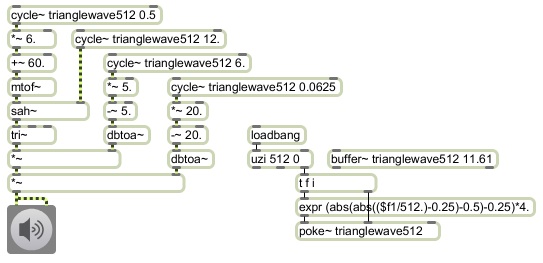
The program is exactly like the example of using a triangle wave as a control function for a pitch glissando, except with a sah~ object inserted to convert the glissando into a scalewise series of discrete constant pitches. The cycle~ object going into the right inlet of sah~ has a frequency of 12 Hz, and it uses the triangle waveform stored in the buffer~ which increases past 0 at the beginning of each cycle. That triggers sah~ to sample and hold the current value of the pitch signal coming in the left intlet. So, whereas the pitch control oscillator is sending out a continuous glissando,

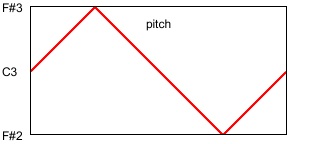
the sah~ object sends out a scalewise rendition of that shape by sampling and holding the pitch only once every 1/12 of a second.

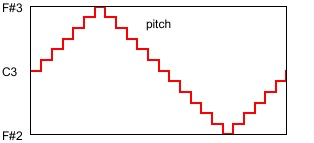
The triangle shape is preserved, but the pitch is now in discrete steps of the chromatic scale at a rate of 12 notes per second instead of being a continuous glissando that changes pitch slightly with every sample. You can see that classic waveforms of electronic music synthesis can be applied in this way to serve as a control function even when the desired effect is individual notes of the tempered 12-tone scale.