Tempo-relative timing

The time interval between events can be expressed as an amount of absolute time, such as a number of milliseconds. In the case of regularly repeating events, the time interval between successive events is constant, and that time interval is called the period. (The events are periodic.) We can say that an event occurs once every [period] milliseconds.

The inverse of the period (1 divided by the period) is called the rate or--especially for repetitions at an audio rate, such as repetitions of a waveform--the frequency. Audio frequency is usually expressed in waveform cycles per second, a.k.a. Hertz, abbreviated Hz.

-----

Here are a couple of examples of calculating rate (or frequency) and period.

An oboe playing the note A above middle C--the note to which the orchestra tunes--produces a tone that consists of a repeating waveform that completes 440 repetitions per second. That's why you often hear musicians refer to "A-440" as a reference tone. The waveform repeats 440 times per second, so its fundamental frequency is 440 Hz (cycles per second), so its period is 1/440 seconds per cycle, which is 0.00227 seconds, i.e., 2.27 milliseconds. Most of the time we care more about a tone's frequency because that determines its perceived pitch; but in computer music, where we're often dealing with sound at a microscopic level, we sometimes need to know its period.

If a short note repeats every quarter note (i.e., every beat) at the rate of 100 beats per minute (100 bpm, a fairly quick rate), its rate is 100 beats per 60 seconds, i.e., 100/60 beats per second, so its period--the time between the onset of each note--is the inverse of that, i.e., 60/100 of a second per beat, i.e. 0.6 seconds, i.e., 600 ms. So if we wanted an echo of each note to occur exactly in between the notes--on the eighth note between each quarter note--we'd know that we need to delay the sound by 1/2 of 600 ms, which is 300 ms.

If we are editing a video with a frame rate of 30 frames per second (30 fps), we can express the rate as 30 frames / 1 second, so the period is the inverse of that: 1 second / 30 frames (i.e., 1/30 of a second per frame), so we know that the time spent on each frame is 1/30 second, i.e., 0.03333 sec., i.e., 33.33 ms.

So here's a problem to test your understanding. If a video with a frame rate of 30 fps is accompanied by music with a beat rate of 100 bpm, how many frames elapse with each beat of the music? We know that the period of the beat is 600 ms, and the period of the video frames is 33.33 ms, so we simply need to calculate how many times 33.33 goes into 600 to find out the number of frames per beat. 600/33.33 = 18. So at that beat rate, a quarter note is equal to 18 frames of video, an eighth note is equal to 9 frames, a triplet eighth notes is equal to 6 frames, and so on.

-----

The measurement of time in seconds or milliseconds is objective and empirical, but there's nothing about those units of measure that has any inherent relationship to human perception, and it's not necessarily always the most useful way to discuss time for musical purposes.

In most music there is some sense of a steady periodic beat. (As with all generalizations regarding music, exceptions are easy to find, but let's accept the statement for the time being.) For most human-performed music, the empirical steadiness or constancy of the beat rate is dubious in actual practice; musicians slow down and speed up all the time, both consciously and unconsciously. But even when the music involves subtle accelerations and decelerations, the musicians are generally working with an understanding of (and, if there are multiple musicians playing, a consensus about) a conceptual constant beat rate in the music, which is somehow being exemplified by the sound. The beat rate is measurable in absolute time, but musicians mostly know and feel the beat rate intuitively, without measuring it by a clock. Once the beat rate is established in the mind of a musician or a listener, other events, rates, and periods are intuitively calculated relative to the beat rate, rather than by absolute clock time. So...

For musical purposes, it's often most useful to establish the beat rate, a.k.a., the tempo, and then think of all units of time relative to that tempo. This is reflected in Western music notation, in which durations are notated relative to a beat, but the rhythmic notation is independent of the tempo, which is written at the beginning of the piece or section. Once we establish a tempo and we call the beat a quarter note, then we can discuss durations and time intervals in terms of note values such as sixteenth note, whole note, etc. without needing to make a direct reference to clock time. This way of discussing time is called tempo-relative time, as opposed to absolute (clock) time. If we change the tempo but keep the tempo-relative notation the same, the absolute time intervals change, but the ratio relationships of those time intervals stay the same. If the beat tempo is known, such as "quarter note = 100" (100 bpm), then it's possible to calculate all tempo-relative time intervals as absolute time intervals, and vice versa. The advantage of using tempo-relative time notation is that a) it's the way musicians traditionally think of time, b) it makes time relationships evident because they're expressed as simple ratios, and c) it allows rhythm and tempo to be expressed independently. In computer music, this has the advantage that by changing a single number--the tempo--we can change the absolute timing of all rhythms while leaving their tempo-relative timing the same.

This program shows how to create timed repetition of an event in Max, using tempo-relative timing.

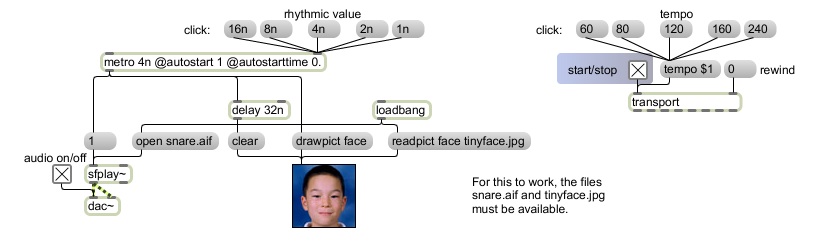
[Note that for this program to work properly, it needs to be able to access two other files, a sound file and an image file. You should download these two (very small) media files -- snare.aif and tinyface.jpg -- and place them in the same folder as the program file.]

This program is the same as the program in the previous lesson on timed repetition at a steady rate, but it expresses time intervals using a central clock, known as the transport in Max, instead of absolute time in milliseconds.

In the upper-right portion of the window is the transport object. When it is started, it provides a central clock that keeps track of the passage of time both in absolute time (milleseconds) and tempo-relative time based on its tempo attribute (measures, beats, and ticks). By default its tempo is 120 bpm, but the tempo can be changed by sending it a new tempo message (such as tempo 80).

This allows other timing objects such as metro to use tempo-relative descriptors for time intervals. For example, if metro receives an interval of 4n (quarter note), it refers to the tempo of the transport (say, 120 bpm) and calculates the correct time interval (in this case, 500 ms). If the tempo of the transport changes, the absolute time interval of the metro would change, even though its tempo-relative interval of 4n remains the same.

The use of tempo-relative time descriptors gives us two ways to change the rate of the metro (or other timing objects in Max). One is to send a new note value to metro (such as 8n if we want it to send output every eighth note). The other is to change the tempo (by sending a different tempo message to the transport).

Unlike the previous program, where there was a toggle switch to turn the metro on and off, in this example the metro's autostart attribute is turned on (autostart 1) which means that it will start whenever the transport is started.

This program shows two different kinds of events, one sonic and one visual. Whereas the previous example used a sonic click (a click~ object) and a flashing button (the flashing capability is built into the button object), this example plays a sound file and shows a picture file. The files that the program accesses have to be in the same folder as the program, or at least somewhere in Max's file search path. When the program is first opened, the loadbang object triggers messages that open the files and get them ready for use.

In the previous program, the click is a sound of minimal duration (1 sample) and the flash of the button is also a very short amount of time, so there was no need to turn them off to get ready for the next event. When playing a soundfile or showing a picture, however, it might be necessary to turn off the sound and erase the picture before the next event, just so that the next event will be noticeable. (For example, if we show a picture that's already being shown, there will be no visible effect.) The snare drum sound is already short and percussive, so even if it's not done playing by the time of the next event, the new percussive attack will make it evident that it has restarted. For the picture, though, we have included automatic erasure after a 32nd note has elapsed. As soon the picture is shown (with the drawpict message), we schedule an erasure to happen a 32nd note later (delay 32n to trigger a clear message).

-----

Here's another question to test your understanding of tempo-relative timing. When the tempo is 120, for how long is the picture displayed in absolute time? When the tempo is 60? 240? Well, there are 60,000 milliseconds per minute, and 120 beats per minute, so there are 60,000/120 milliseconds per beat, i.e., 500 ms per 4n. A 32nd note is 1/8 of a quarter note, so its absolute time duration will be 1/8 of 500 ms, i.e. 62.5 ms. When the tempo is 60, the duration of 32n is 125 ms, and when the tempo is 240 the duration of 32n is 31.25 (i.e., 1/32 of a second, which is about the duration of a single frame of video).

-----

While we're on the subject of turning things off, this might be a good time to distinguish between duration--how long something lasts--and inter-onset interval (IOI) which is a cognitive science term for the time interval between beginnings of events. In this case, the rate of the metro determines the inter-onset interval (500 ms when the note value is 4n and the tempo is 120), but the program has been written to make the duration of the picture's display be always a 32nd note (62.5 ms when the tempo is 120). Thus the duration of the picture is independent of the inter-onset interval (the time interval between drawpict messages).